In nature, almost all turbulent flows are invariably ‘unsteady‘. What is prescribed as ‘steady‘ is the statistical averaged variable, provided that the flow has an energy equilibrium condition. In such cases, one correct formulation is the steady RANS.
Other pure unsteady statistical formulations exist, such as unsteady RANS (URANS).
In a specific flow problem, viz. flow around a bluff body, it is difficult to get a good solution for drag using RANS. The LES or hybrid DES formulations better address this type of problem.
Every system has a steady and a transient state. The steady-state of the system is reached when the state does not change its value in successive iterations. The transient state is the phase between the beginning and till steady state that has been achieved.
A 2D steady-state heat conduction equation:
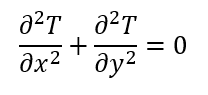
A 2D transient state heat conduction equation:
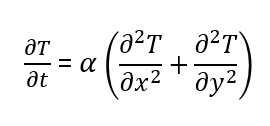
Some of the steady-state methods are:
- Jacobi method
- Gauss-Seidel method
- SOR method
Crank-Nicholson methods are used for transient state calculation.
SOR should be used in the steady-state analysis because it converges in fewer iterations and has lesser memory requirements than Jacobi.
In transient state analysis, the explicit scheme is faster. A steady-state solver is faster because of the mathematical simplification. There is no thermal diffusivity and no time integration. There will be no numerical diffusion, and the solution will always be stable, just that we have to choose a good CFL/courant number. (Courant No. = v * dt /dl, where, v = velocity of flow, dt= time step, dl = grid cell size).
