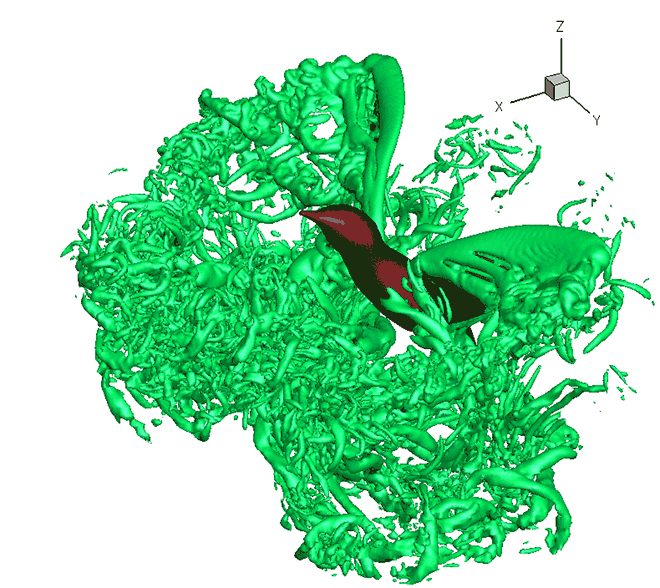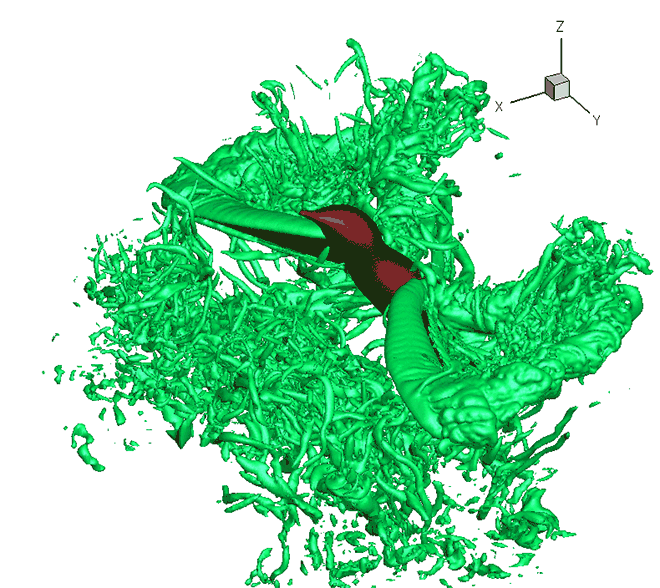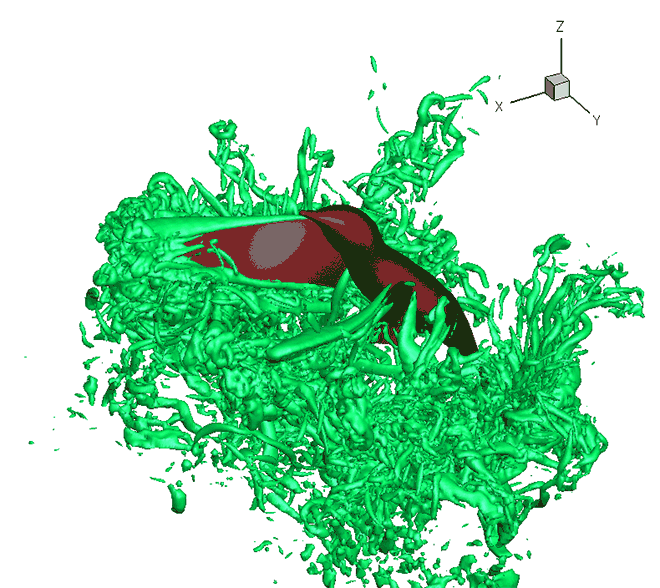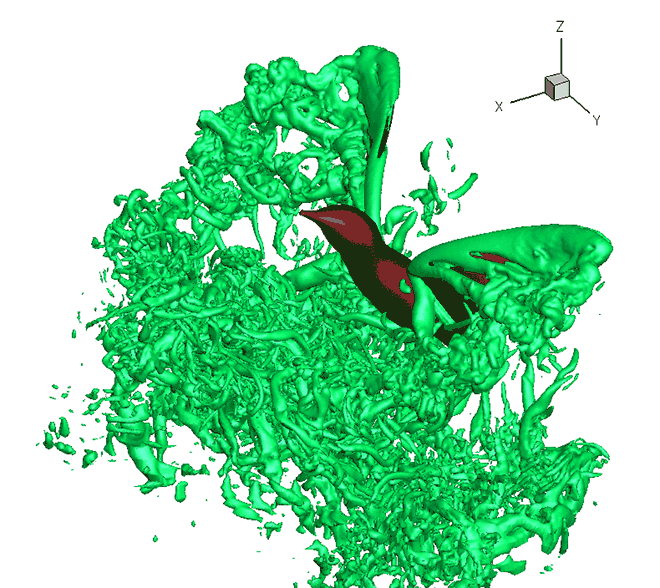
The aerodynamic surfaces (viz. wings) are generally considered to be in steady condition (i.e. time-invariant) and thus the resulting forces and moments are also ‘steady’ (i.e. no change with time). However, this assumption has limitations at various critical flight conditions, such as, during maneuver and gust response analyses the behavior of aerodynamic surfaces under dynamic motion is required and it is necessary to include the effect of the aerodynamic surface motion upon the resulting forces and moments.
These so-called ‘unsteady’ effects are an outcome of the changing circulation and wake acting upon a moving aerofoil wing, and can have significant considerable influence upon the resulting aerodynamic forces and moments. A more detailed and sophisticated analysis is required than simply considering the angle of incidence.
Theodorsen model
Pioneering work has been carried out by Wagner, Prandtl, Theodorsen, and Garrick described some fundamental physical concepts in understanding and modeling unsteady aerodynamics. These concepts are usually incorporated with a potential flow approach and small disturbance theory to obtain analytical expressions of flow quantities. The unsteady lift on a harmonically oscillating airfoil in incompressible flow has been studied by Kussner and Schwarz , but the most well-known solution is due to Theodorsen . The lift on a thin rigid airfoil under-going oscillatory motion can be written as:
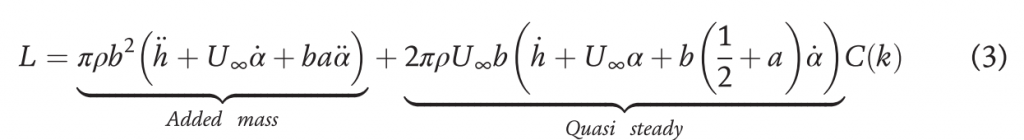
In normalized form,
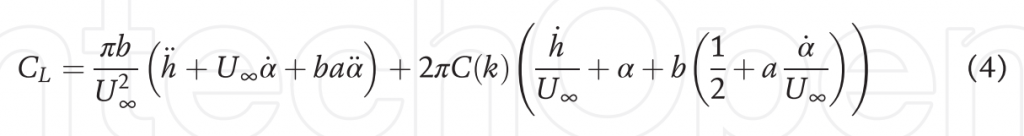where, h_dot_dot and alpha_dot_dot are plunging and pitching accelerations respectively. The first group of terms are the non-circulatory components that account for the fluid inertia (added mass force). The second group of terms are the circulatory components, where C(k) accounts for the influence of the shed wake vorticity (lift deficiency factor).
Since the Theodorsen function necessitates a periodic motion for its input parameters (e.g. angle of attack or quasi-steady lift), a Fourier transform should be applied to the pitch ramp maneuver under study. The effective angle of attack of the proposed ramp pitch motion can be written as:
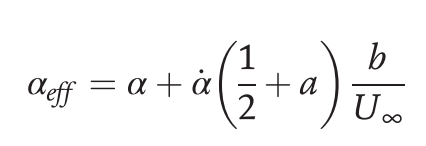
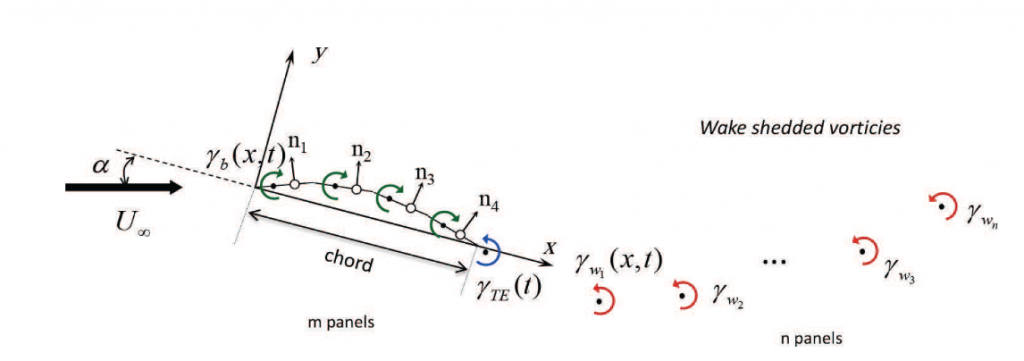
Unsteady Vortex Lattice Method
The unsteady Vortex lattice methods (UVLMs) are well suited to the bio-inspired flight problems because they can account for the circulation distribution variations on wings, the velocity potential time-dependency, and the shedding of wake downstream. Although they are considered low fidelity models, they may be extended to capture unconventional lift mechanisms such as leading-edge vortex. These discrete vortex models are widely used in modeling aerodynamics of aircraft and rotorcraft analysis, compared to computational fluid dynamics (CFD) models which are more computationally expensive. The use of the UVLM method is now a powerful tool in hand for aerodynamicists for its ease of implementation even for complex shapes.
