LQR control design is recently becoming quiet popular in aerospace vehicle design. While there are several literature available in LQR theory and applications, little is talked about the selection of the Q & R weights in the design phase…and thus this article. LQR design method mainly concerns stabilizing and controlling a dynamic system,viz, fighter aircraft,rocket at minimum cost.
As a starting point, we can consider R=1 and Q=1/τ ^2*ld (τ has the dimension of a time).
If τ is small, the closed-loop system gets faster, but at the expense of a large control effort.
If τ is large, it’s the other way round.
There are many other, and possibly better, ways to chose Q.
For instance, you can use the partial Controllability Gramian.
Choosing LQR weights:
One of the critical design step in LQR methodology is choosing the weights of Q and R. Apriori knowledge of the system open-loop response is required and the performance objectives to choose specific values for the cost function weight Q and R.
One of the method is to choose diagonal weights as presented below.
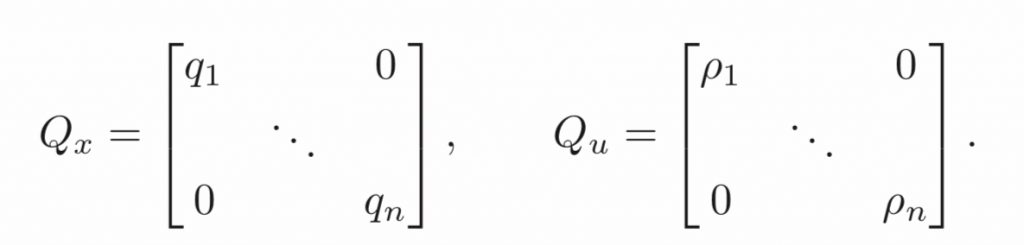
For the choice of Q and R, the individual diagonal elements would describe how much each state and input (squared) should contribute to the overall cost function.
Hence, we can consider states that should remain small and attach higher weight values to them. Similarly, we can penalize an input versus the states and other inputs through choice of the corresponding input weight ρj.
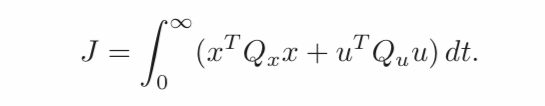
- Choose qi and ρj as the inverse of the square of the maximum value for the corresponding xi or uj;
- Modify the elements to obtain a trade-off between response time, damping and control effort. This second step can be performed by trial and error.
Some additional points:
- The main idea in LQR control design is to minimize the quadratic cost function of int(x^TQx + u^TRu)dt.
- It turns out that regardless of the values of Q and R, the cost function has a unique minimum that can be obtained by solving the Algebraic Riccati Equation(ARE).
- The parameters Q and R are the design parameters to penalize the state variables(x) and the control signals(u).
- The larger these values are, the more you penalize these signals.
- Choosing a large value for R means to try to stabilize the system with less (weighted) energy. This is often called expensive control strategy.
- Choosing a small value for R means you don’t want to penalize the control signal, often referred as cheap control strategy.
- Similarly, choosing a large value for Q means to try stabilize the system with the least possible changes in the states and large Q implies less concern about the changes in the states.
- Since there is a trade-off between the two, we keep Q as I (identity matrix) and only alter R.
- A large R can be chosen if there is a limit on the control output signal, viz. large control signals introduce sensor noise / cause actuator’s saturation.
- Quiet often, in tactical missile system design, required power may not be adequately available from the system due to stringent constraints in power, space and volume requirements.

SB | Nov 22, 2020